Calcule standard și normale ale distribuției Excel
 Share
Share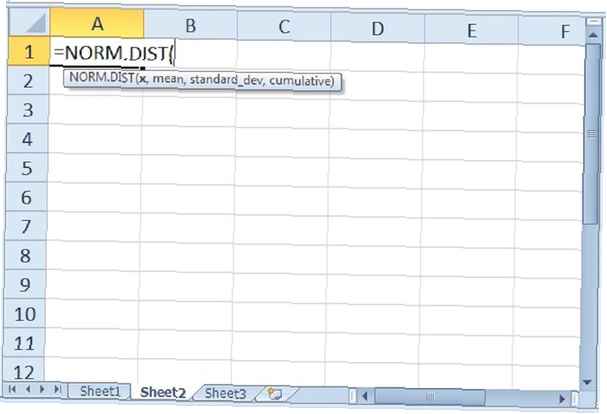
Aproape orice pachet software statistic poate fi utilizat pentru calcule referitoare la o distribuție normală, mai frecvent cunoscută sub numele de curbă de clopot. Excel este echipat cu o multitudine de tabele și formule statistice și este destul de simplu să folosiți una dintre funcțiile sale pentru o distribuție normală. Vom vedea cum se utilizează funcțiile NORM.DIST și NORM.S.DIST în Excel.
Distribuții normale
Există un număr infinit de distribuții normale. O distribuție normală este definită de o anumită funcție în care au fost determinate două valori: media și abaterea standard. Media este orice număr real care indică centrul distribuției. Abaterea standard este un număr real pozitiv, care este o măsură a distribuției. Odată ce cunoaștem valorile mediei și abaterii standard, distribuția normală specială pe care o utilizăm a fost complet determinată.
Distribuția normală standard este o distribuție specială din numărul infinit de distribuții normale. Distribuția normală standard are o medie de 0 și o abatere standard de 1. Orice distribuție normală poate fi standardizată la distribuția normală standard printr-o formulă simplă. Acesta este motivul pentru care, de obicei, singura distribuție normală cu valori depuse este aceea a distribuției normale standard. Acest tip de tabel este uneori denumit tabel de scoruri z.
NORM.S.DIST
Prima funcție Excel pe care o vom examina este funcția NORM.S.DIST. Această funcție returnează distribuția normală standard. Există două argumente necesare pentru funcție: „z”Și„ cumulativ ”. Primul argument al lui z este numărul abaterilor standard depărtate de medie. Asa de, z = -1,5 este o abateri standard și jumătate sub medie. z-scorul de z = 2 este două abateri standard peste medie.
Al doilea argument este cel al „cumulativului”. Există două valori posibile care pot fi introduse aici: 0 pentru valoarea funcției de densitate a probabilității și 1 pentru valoarea funcției de distribuție cumulată. Pentru a determina zona de sub curbă, vom dori să introducem un 1 aici.
Exemplu
Pentru a ajuta să înțelegem cum funcționează această funcție, vom analiza un exemplu. Dacă facem clic pe o celulă și introducem = NORM.S.DIST (.25, 1), după lovirea intră, celula va conține valoarea 0,5987, care a fost rotunjită la patru zecimale. Ce inseamna asta? Există două interpretări. Primul este că zona de sub curbă pentru z mai mic sau egal cu 0,25 este 0,5987. A doua interpretare este aceea că 59,87 la sută din suprafața de sub curba pentru distribuția normală normală apare atunci când z este mai mică sau egală cu 0,25.
NORM.DIST
A doua funcție Excel pe care o vom analiza este funcția NORM.DIST. Această funcție returnează distribuția normală pentru o medie specificată și o abatere standard. Pentru această funcție sunt necesare patru argumente: „X,”„ Înseamnă ”,„ abatere standard ”și„ cumulativ ”. Primul argument al lui X este valoarea observată a distribuției noastre. Media și abaterea standard sunt explicative de la sine. Ultimul argument al „cumulativului” este identic cu cel al funcției NORM.S.DIST.
Exemplu
Pentru a ajuta să înțelegem cum funcționează această funcție, vom analiza un exemplu. Dacă facem clic pe o celulă și introducem = NORM.DIST (9, 6, 12, 1), după ce ați intrat, celula va conține valoarea 0,5987, care a fost rotunjită la patru zecimale. Ce inseamna asta?
Valorile argumentelor ne spun că lucrăm cu distribuția normală care are o medie de 6 și o abatere standard de 12. Încercăm să determinăm ce procent din distribuție are loc X mai mică sau egală cu 9. În mod echivalent, dorim zona de sub curba acestei distribuții normale și spre stânga liniei verticale X = 9.
NORM.S.DIST vs NORM.DIST
Există câteva lucruri de notat în calculele de mai sus. Vedem că rezultatul pentru fiecare dintre aceste calcule a fost identic. Acest lucru se datorează faptului că 9 este 0.25 abateri standard peste media de 6. Am fi putut converti prima dată X = 9 în a z-scor de 0,25, dar software-ul face acest lucru pentru noi.
Celălalt lucru de remarcat este faptul că nu avem nevoie de ambele formule. NORM.S.DIST este un caz special al NORM.DIST. Dacă lăsăm media egală cu 0 și abaterea standard egală cu 1, atunci calculele pentru NORM.DIST se potrivesc cu cele ale NORM.S.DIST. De exemplu, NORM.DIST (2, 0, 1, 1) = NORM.S.DIST (2, 1).
