Regula de completare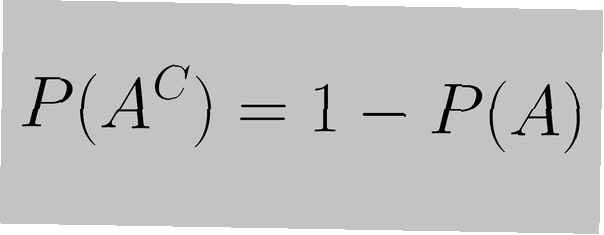

În statistici, regula complementului este o teoremă care oferă o conexiune între probabilitatea unui eveniment și probabilitatea complementului evenimentului, astfel încât dacă cunoaștem una dintre aceste probabilități, atunci o cunoaștem automat pe cealaltă.

Regula complementului este utilă atunci când calculăm anumite probabilități. De multe ori probabilitatea unui eveniment este dezordonată sau complicată de calculat, în timp ce probabilitatea complementului său este mult mai simplă.

Înainte de a vedea cum este utilizată regula complementului, vom defini în mod specific care este această regulă. Începem cu un pic de notație. Complementul evenimentului A, format din toate elementele din spațiul de probă S care nu sunt elemente ale setului A, este notat de AC.

Declarația regulii de completare

Regula complementului este declarată „suma probabilității unui eveniment și probabilitatea complementului său este egală cu 1”, așa cum este exprimată prin următoarea ecuație:

P (A^C) = 1 - P (A)

Următorul exemplu va arăta cum se utilizează regula complementului. Va deveni evident că această teoremă va accelera și va simplifica calculele de probabilitate.

Probabilitate fără regula complementului

Să presupunem că aruncăm opt monede corecte - care este probabilitatea ca noi să avem cel puțin un cap? O modalitate de a descoperi acest lucru este de a calcula următoarele probabilități. Numitorul fiecăruia se explică prin faptul că există 2⁸ = 256 rezultate, fiecare la fel de probabil. Toate următoarele ne oferă o formulă pentru combinații:

• Probabilitatea de a răsuci exact un cap este C (8,1) / 256 = 8/256.
• Probabilitatea de a răsuci exact două capete este C (8,2) / 256 = 28/256.
• Probabilitatea de a răsuci exact trei capete este C (8,3) / 256 = 56/256.
• Probabilitatea de a răsuci exact patru capete este C (8,4) / 256 = 70/256.
• Probabilitatea de a răsuci exact cinci capete este C (8,5) / 256 = 56/256.
• Probabilitatea de a răsuci exact șase capete este C (8,6) / 256 = 28/256.
• Probabilitatea de a răsuci exact șapte capete este C (8,7) / 256 = 8/256.
• Probabilitatea de a rasturna exact opt ​​capete este C (8,8) / 256 = 1/256.

Acestea sunt evenimente care se exclud reciproc, deci rezumăm împreună probabilitățile folosind una dintre regulile de adăugare corespunzătoare. Aceasta înseamnă că probabilitatea ca noi să avem cel puțin un cap să fie 255 din 256.

Utilizarea regulii de completare pentru a simplifica problemele de probabilitate

Acum calculăm aceeași probabilitate folosind regula complementului. Complementul evenimentului „Răsturnăm cel puțin un cap” este evenimentul „Nu există capete”. Există o modalitate de a se întâmpla acest lucru, oferindu-ne probabilitatea de 1/256. Folosim regula complementului și descoperim că probabilitatea noastră dorită este una minus una din 256, care este egală cu 255 din 256.

Acest exemplu demonstrează nu numai utilitatea, ci și puterea regulii complementului. Deși nu este nimic în neregulă cu calculul inițial, acesta a fost destul de implicat și a necesitat mai multe etape. În schimb, atunci când am folosit regula complementului pentru această problemă, nu au existat atât de mulți pași în care calculele ar putea merge prost.