Teoria de seturi

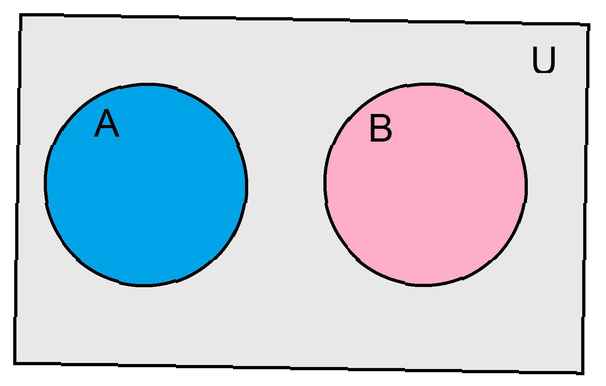
Teoria seturilor este un concept fundamental în toată matematica. Această ramură a matematicii constituie o bază pentru alte subiecte. 

Intuitiv un set este o colecție de obiecte, care se numesc elemente. Deși acest lucru pare o idee simplă, aceasta are unele consecințe de anvergură. 

element

Elementele unui set pot fi cu adevărat orice - numere, stări, mașini, oameni sau chiar alte seturi sunt toate posibilitățile pentru elemente. Aproape orice poate fi colectat împreună poate fi folosit pentru a forma un set, deși există anumite lucruri la care trebuie să fim atenți.

Seturi egale

Elementele unui set sunt fie într-un set, fie nu într-un set. Putem descrie un set printr-o proprietate definitorie sau putem enumera elementele din set. Ordinea în care sunt enumerate nu este importantă. Deci seturile 1, 2, 3 și 1, 3, 2 sunt seturi egale, deoarece ambele conțin aceleași elemente.

Două seturi speciale

Două seturi merită menționate în mod special. Primul este setul universal, notat în mod obișnuit U. Acest set reprezintă toate elementele din care putem alege. Acest set poate fi diferit de la o setare la alta. De exemplu, un set universal poate fi setul de numere reale, în timp ce pentru o altă problemă setul universal poate fi numerele întregi 0, 1, 2, .... 

Celălalt set care necesită o anumită atenție se numește set gol. Setul gol este setul unic este setul fără elemente. Putem scrie acest lucru ca și denota acest set prin simbolul ∅.

Subseturile și setul de alimentare

O colecție a unora dintre elementele unui set A se numește subset de A. Spunem asta A este un subset de B dacă și numai dacă fiecare element al A este de asemenea un element al B. Dacă există un număr finit n de elemente dintr-un set, apoi sunt în total 2ⁿ subseturi de A. Această colecție a tuturor subseturilor din A este un set care se numește setul de putere al A.

Setați operațiuni

La fel cum putem efectua operațiuni precum adăugarea - pe două numere pentru a obține un număr nou, operațiile de teorie a seturilor sunt utilizate pentru a forma un set din alte două seturi. Există o serie de operații, dar aproape toate sunt compuse din următoarele trei operații:

• Uniune - O uniune semnifică reunirea. Unirea seturilor A și B constă din elementele care sunt în oricare A sau B.
• Intersecție - O intersecție este locul în care se întâlnesc două lucruri. Intersecția seturilor A și B constă din elementele care în ambele A și B.
• Complement - Complementul setului A constă din toate elementele din setul universal care nu sunt elemente din A.

Diagrame Venn

Un instrument care este util în a descrie relația dintre diferite seturi se numește diagrama Venn. Un dreptunghi reprezintă setul universal pentru problema noastră. Fiecare set este reprezentat cu un cerc. Dacă cercurile se suprapun între ele, atunci aceasta ilustrează intersecția celor două seturi noastre. 

Aplicații din teoria seturilor

Teoria seturilor este folosită în întreaga matematică. Este folosit ca bază pentru multe subcâmpuri ale matematicii. În domeniile referitoare la statistici, este utilizat în special în probabilitate. O mare parte din concepte în probabilitate provin din consecințele teoriei de seturi. Într-adevăr, o modalitate de a afirma axiomele probabilității implică teoria seturilor.