Numărul Pi 3.14159265 ...

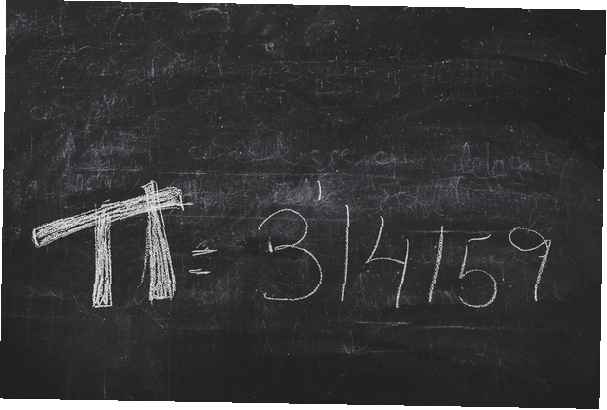
Una dintre cele mai utilizate pe scară largă de-a lungul matematicii este numărul pi, care este notat cu litera greacă π. Conceptul de pi își are originea în geometrie, dar acest număr are aplicații de-a lungul matematicii și apare la subiecte de anvergură, inclusiv statistici și probabilitate. Pi chiar a câștigat recunoașterea culturală și propria sărbătoare, cu celebrarea activităților de Ziua Pi în toată lumea.

Valoarea lui Pi

Pi este definit ca raportul circumferinței unui cerc față de diametrul său. Valoarea pi este puțin mai mare decât trei, ceea ce înseamnă că fiecare cerc din univers are o circumferință cu o lungime care este puțin mai mare de trei ori diametrul său. Mai precis, pi are o reprezentare zecimală care începe 3.14159265 ... Aceasta este doar o parte din expansiunea zecimală a pi.

Fapte Pi

Pi are multe caracteristici fascinante și neobișnuite, inclusiv: 

• Pi este un număr real irațional. Aceasta înseamnă că pi nu poate fi exprimată ca o fracție a / b Unde A și b sunt ambii numere întregi. Deși numerele 22/7 și 355/113 sunt utile în estimarea pi, niciuna dintre aceste fracțiuni nu este adevărata valoare a pi.
• Deoarece pi este un număr irațional, expansiunea sa zecimală nu se termină nici nu se repetă. Există câteva întrebări cu privire la această expansiune zecimală, cum ar fi: apare fiecare șir de cifre posibil undeva în expansiunea zecimală a pi? Dacă apare toate șirurile posibile, numărul dvs. de telefon mobil este undeva în expansiunea pi (dar la fel este și toți ceilalți).
• Pi este un număr transcendental. Aceasta înseamnă că pi nu este zero al unui polinom cu coeficienți întregi. Acest fapt este important atunci când explorezi caracteristicile mai avansate ale pi.
• Pi este important din punct de vedere geometric și nu doar pentru că raportează circumferința și diametrul unui cerc. Acest număr apare și în formula pentru zona unui cerc. Zona unui cerc de rază r este A = pi r². Numărul pi este utilizat în alte formule geometrice, cum ar fi suprafața și volumul unei sfere, volumul unui con și volumul unui cilindru cu o bază circulară.
• Pi apare când este cel puțin așteptat. Pentru unul dintre numeroasele exemple de acest lucru, luați în considerare suma infinită 1 + 1/4 + 1/9 + 1/16 + 1/25 + ... Această sumă converg la valoarea pi²/ 6.

Pi în statistici și probabilitate

Pi face apariții surprinzătoare de-a lungul matematicii, iar unele dintre aceste apariții sunt în subiecte de probabilitate și statistici. Formula pentru distribuția normală, cunoscută și sub numele de curba clopotului, prezintă numărul pi ca o constantă de normalizare. Cu alte cuvinte, împărțirea printr-o expresie care implică pi vă permite să spuneți că zona de sub curbă este egală cu una. Pi face parte din formulele pentru alte distribuții de probabilitate.

O altă apariție surprinzătoare a probabilității pi este un experiment de aruncare a acului vechi de secole. În secolul al XVIII-lea, Georges-Louis Leclerc, Comte de Buffon a pus o întrebare cu privire la probabilitatea căderii ace: Începeți cu o podea cu scânduri de lemn cu o lățime uniformă în care liniile dintre fiecare dintre scânduri sunt paralele între ele. Luați un ac cu o lungime mai mică decât distanța dintre scânduri. Dacă aruncați un ac pe podea, care este probabilitatea ca acesta să aterizeze pe o linie între două dintre scândurile din lemn?

După cum se dovedește, probabilitatea ca acul să aterizeze pe o linie între două scânduri este de două ori lungimea acului împărțită la lungimea între scândurile de mai multe ori.