Efectul fotoelectric

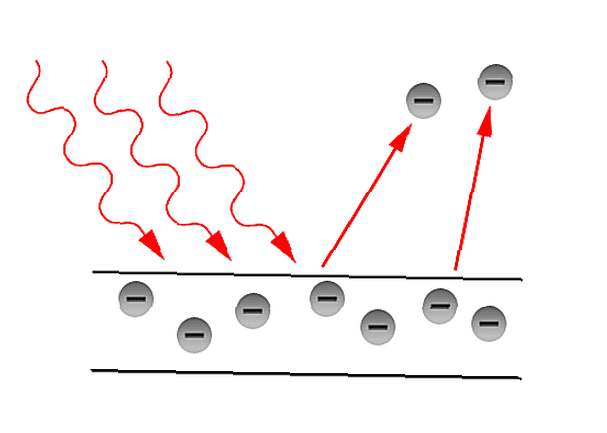
efect fotoelectric a reprezentat o provocare semnificativă pentru studiul opticii în ultima parte a anilor 1800. A contestat teoria valurilor clasice de lumină, care era teoria dominantă a vremii. A fost soluția acestei dileme fizice care l-a catapultat pe Einstein în proeminența în comunitatea fizică, câștigându-i în cele din urmă Premiul Nobel din 1921.

Care este efectul fotoelectric?

Annalen der Physik

Când o sursă de lumină (sau, mai general, radiații electromagnetice) este incidentă pe o suprafață metalică, suprafața poate emite electroni. Electronii emisi în acest mod sunt numiți fotoelectronilor (deși sunt în continuare doar electroni). Acest lucru este ilustrat în imaginea din dreapta.

Configurarea efectului fotoelectric

Administrând un potențial negativ de tensiune (cutia neagră din imagine) colectorului, este nevoie de mai multă energie pentru ca electronii să finalizeze călătoria și să inițieze curentul. Punctul în care niciun electron nu-l face colector se numește oprirea potențialului V_s, și poate fi utilizat pentru a determina energia cinetică maximă K_max a electronilor (care au sarcină electronică e) folosind următoarea ecuație:

K_max = eV_s

Explicația valului clasic

Funcția Iwork phiPhi

Trei predicții principale provin din această explicație clasică:

1. Intensitatea radiației ar trebui să aibă o relație proporțională cu energia cinetică maximă rezultată.
2. Efectul fotoelectric ar trebui să apară pentru orice lumină, indiferent de frecvență sau lungime de undă.
3. Ar trebui să existe o întârziere în ordinea de secunde între contactul radiației cu metalul și eliberarea inițială a fotoelectronilor.

Rezultatul experimental

1. Intensitatea sursei de lumină nu a avut niciun efect asupra energiei cinetice maxime a fotoelectronilor.
2. Sub o anumită frecvență, efectul fotoelectric nu apare deloc.
3. Nu există nicio întârziere semnificativă (sub 10)^-9 s) între activarea sursei de lumină și emisia primilor fotoelectroni.

După cum puteți spune, aceste trei rezultate sunt exact opusul predicțiilor teoriei undelor. Nu numai asta, dar toate sunt complet contra-intuitive. De ce lumina de joasă frecvență nu ar declanșa efectul fotoelectric, deoarece încă mai transportă energie? Cum se eliberează fotoelectronii atât de repede? Și, poate cel mai curios, de ce adăugarea mai multă intensitate nu are ca rezultat eliberarea de electroni mai energică? De ce teoria undelor nu reușește atât de mult în acest caz atunci când funcționează atât de bine în atâtea alte situații

Anul minunat al lui Einstein

Albert Einstein Annalen der Physik

Bazându-se pe teoria radiației lui Black Planck a lui Max Planck, Einstein a propus că energia radiațiilor nu este distribuită continuu pe frontul de undă, ci este în schimb localizată în pachete mici (mai târziu numite fotoni). Energia fotonului ar fi asociată cu frecvența sa (ν), printr-o constantă de proporționalitate cunoscută sub numele de Constanta lui Planck (h), sau alternativ, folosind lungimea de undă (λ) și viteza luminii (c):

E = hν = hc / λ

sau ecuația de moment: p = h / λ