Proprietățile asociative și comutative

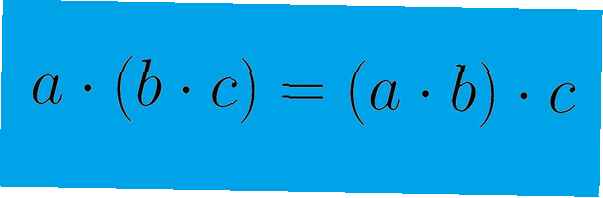
Există mai multe proprietăți matematice care sunt utilizate în statistici și probabilitate; două dintre acestea, proprietățile comutative și asociative, sunt, în general, asociate cu aritmetica de bază a numerelor întregi, raționale și numere reale, deși apar și în matematica mai avansată..

Aceste proprietăți - comutativ și asociativ - sunt foarte similare și pot fi ușor amestecate. Din acest motiv, este important să înțelegem diferența dintre cei doi.

Proprietatea comutativă privește ordinea anumitor operații matematice. Pentru o operație binară - una care implică doar două elemente - acest lucru poate fi arătat prin ecuația a + b = b + a. Operația este comutativă deoarece ordinea elementelor nu afectează rezultatul operației. Proprietatea asociativă, pe de altă parte, privește gruparea elementelor într-o operație. Acest lucru poate fi arătat de ecuația (a + b) + c = a + (b + c). Gruparea elementelor, așa cum este indicat de paranteze, nu afectează rezultatul ecuației. Rețineți că atunci când este utilizată proprietatea comutativă, elementele dintr-o ecuație sunt rearanjată. Când se utilizează proprietatea asociativă, elementele sunt doar regrupat.

Comutativitate

Mai simplu spus, proprietatea comutativă afirmă că factorii dintr-o ecuație pot fi rearanjați liber, fără a afecta rezultatul ecuației. Prin urmare, proprietatea comutativă se referă la ordonarea operațiunilor, inclusiv la adăugarea și înmulțirea numerelor reale, a numerelor întregi și a numerelor raționale.

De exemplu, numerele 2, 3 și 5 pot fi adăugate împreună în orice ordine, fără a afecta rezultatul final:

2 + 3 + 5 = 10

3 + 2 + 5 = 10

5 + 3 + 2 = 10

De asemenea, numerele pot fi înmulțite în orice ordine, fără a afecta rezultatul final:

2 x 3 x 5 = 30

3 x 2 x 5 = 30

5 x 3 x 2 = 30

Însă scăderea și divizarea nu sunt operații care pot fi comutative, deoarece ordinea operațiilor este importantă. Cele trei numere de mai sus nu poti, de exemplu, scade în orice ordine, fără a afecta valoarea finală:

2 - 3 - 5 = -6

3 - 5 - 2 = -4

5 - 3 - 2 = 0